贝塞尔曲线

贝塞尔曲线奠定了计算机绘图的基础(它可以将任何复杂的图形用精确的数学语言进行描述)
有开放和封闭路径的区别；

理解贝塞尔曲线的原理

贝塞尔曲线是由一系列点来控制曲线状态的

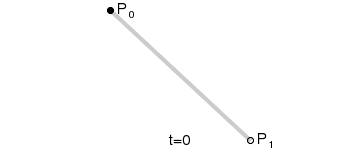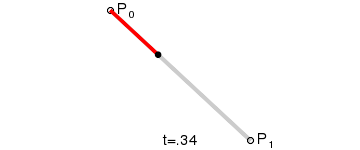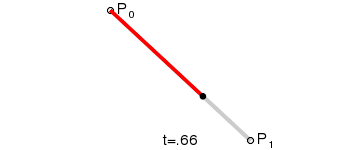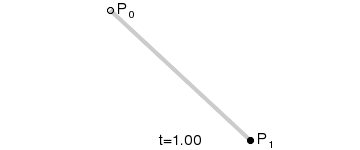
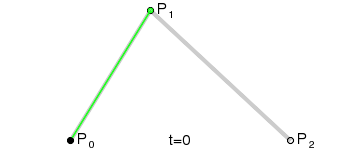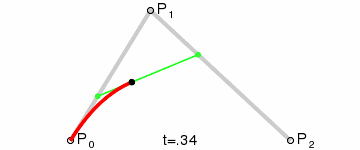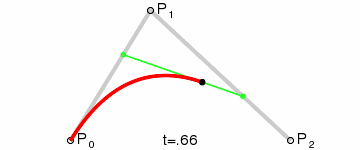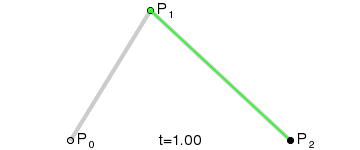
一阶曲线是没有控制点的，仅有两个数据点(A 和 B)，最终效果一个线段；类似于lineTo；

生成过程：

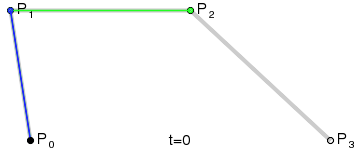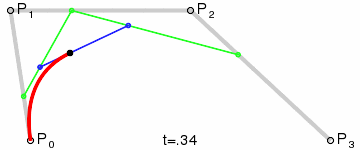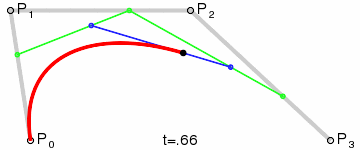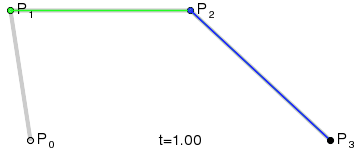
二阶曲线由两个数据点(A 和 C)，一个控制点(B)来描述曲线状态；类似于quadTo；

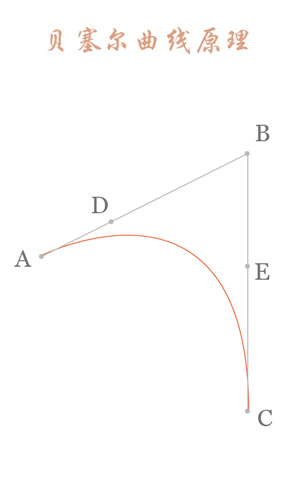
连接AB BC，并在AB上取点D，BC上取点E，使其满足条件：AD/AB = BE/BC
链接DE，取点F，使：AD/AB=BE/BC=DF/DE

生成过程：

三阶曲线由两个数据点(A 和 D)，两个控制点(B 和 C)来描述曲线状态

生成过程：

同lineTo

二阶曲线是由两个数据点，一个控制点构成
两个数据点是控制贝塞尔曲线开始和结束的位置，而控制点则是控制贝塞尔的弯曲状态

1 2	path.moveTo(start.x,start.y); path.quadTo(control.x,control.y,end.x,end.y);

由两个数据点和两个控制点来控制曲线状态

1 2	path.moveTo(start.x, start.y); path.cubicTo(control1.x, control1.y, control2.x,control2.y, end.x, end.y);

贝塞尔曲线的主要优点是可以实时控制曲线状态，并可以通过改变控制点的状态实时让曲线进行平滑的状态变化。